Answer:
The point Q(6,7) lie outside the circle.
Explanation:
We know that, the general equation of a circle,
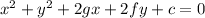 ---------(1)
---------(1)
Centre is (-g, -f) = (2,4) (given)
So, -g = 2⇒g = -2
and, -f = 4⇒f = -4
Putting the value of g and f in equation(1), we get
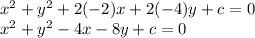
The point L(0,8) is on the circle, the this point can satisfy the above equation.
So,
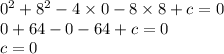
Now, the equation of circle is
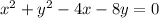
Putting the
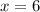 and
and
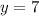 in the above equation, we get
in the above equation, we get
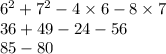
5, which is greater than 0.
So, the point Q(6,7) lie outside the given circle.