Answer:
Null hypothesis:
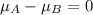
Alternative hypothesis:
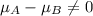
And for this case we can use the confidence interval given by:
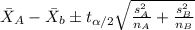
And after calculate the 90% confidence interval we got:

So then we see that all the values are negative so then we can conclude that the two means are different and on this case the mean for A seems to be lower than the mean for B at 10% of significance.
Explanation:
Data given and notation
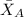 represent the mean for the sample A
represent the mean for the sample A
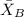 represent the mean for the sample B
represent the mean for the sample B
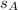 represent the sample standard deviation for the sample A
represent the sample standard deviation for the sample A
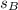 represent the sample standard deviation for the sample B
represent the sample standard deviation for the sample B
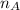 sample size selected A
sample size selected A
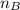 sample size selected B
sample size selected B
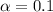 represent the significance level for the hypothesis test.
represent the significance level for the hypothesis test.
t would represent the statistic (variable of interest)
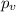 represent the p value for the test (variable of interest)
represent the p value for the test (variable of interest)
State the null and alternative hypotheses.
We need to conduct a hypothesis in order to check if the two means are equal., the system of hypothesis would be:
Null hypothesis:
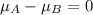
Alternative hypothesis:
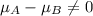
And for this case we can use the confidence interval given by:
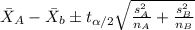
And after calculate the 90% confidence interval we got:

So then we see that all the values are negative so then we can conclude that the two means are different and on this case the mean for A seems to be lower than the mean for B at 10% of significance.