Question

How would you caculate the zeros for this problem ×2- 10×+16=0 ??? I need step by steps for this question

Answer 1

x=2 or x=8

Explanation:

I find it easiest to factor the equation, but you might find it easier to use the quadratic formula. Both will be shown.

Factoring

It is helpful to understand the relationship between the trinomial and its binomial factors:

(x +a)(x +b) = x^2 +(a+b)x +ab

This tells you the constant (ab = 16) will have two factors (a, b) that have a sum equal to the x-coefficient (a+b = -10).

We can list the factorization of 16 to see which factor pairs match that requirement:

16 = -1×-16 = -2×-8 = -4×-4

The sums of these factors are, respectively, -17, -10, -8. The pair with a sum of -10 is the one of interest. This tells us the equation factors as ...

(x -2)(x -8) = 0

The zero product rule tells us that for the product to be zero, one or more of the factors must be zero. The first factor will be zero when x=2; the second factor will be zero for x=8.

The zeros of the quadratic are x=2 or 8.

__

Quadratic Formula

The general form of a quadratic equation is often written as ...

`ax^2+bx+c=0`

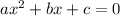
And the general solution of this quadratic is given by the formula ...

`x=(-b\pm√(b^2-4ac))/(2a)`

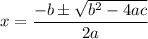
Your equation has a=1, b=-10, c=16, so the quadratic formula gives the zeros as ...

`x=(-(-10)\pm√((-10)^2-4\cdot 1\cdot 16))/(2\cdot 1)=(10\pm√(36))/(2)=5\pm 3`

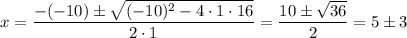
As before, the zeros are 5-3 = 2, and 5+3 = 8.