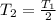Answer:
The orbital period of the planet would be half that of the earth
Step-by-step explanation:
From the question we are told that
The mass of star is four times the mass of sun which can be mathematically represented as

Mathematically gravitational potential is given as

Where M is mass one
m is mass two
From this equation we see that the attraction force is directly proportional to the mass of the star
Thus we can say that

The centrifugal force that balances this attraction Force is
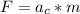
Where
 is the centrifugal acceleration which can be mathematically represented as
is the centrifugal acceleration which can be mathematically represented as
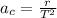
and m is the mass
Substituting this into the equation for centrifugal force
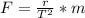
substituting into the equation above
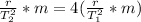
Given that the diameter is the same and assuming that the mass is constant
Then
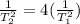
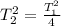
Take square root of both sides