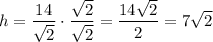Question

Find side lengths C and H

Answer 1

`\displaystyle c=(2√(3))/(3)\\\\\displaystyle h=7√(2)\\`

Explanation:

Right Triangles

A right triangle can be identified by the fact it has an internal angle of 90°. In a right triangle, the trigonometric ratios stand.

Let's consider the triangle to the left. We need to calculate side c, one of the legs of the triangle. We can use the angle adjacent to it (60°) or the angle opposite to it (30°) with the appropriate trigonometric ratio.

We'll use the adjacent angle, and

`\displaystyle tan60^o=(2)/(c)`

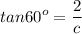
Solving for c

`\displaystyle c=(2)/(tan60^o)=(2)/(√(3))`

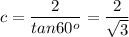
Rationalizing

`\displaystyle c=(2)/(√(3))\cdot (√(3))/(√(3))=(2√(3))/(3)`

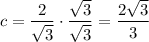
Now for the triangle to the right. The side h is the hypotenuse. Again, any of the two angles can be used (though they are equal, for it's an isosceles triangle). For any of them it is true that

`\displaystyle sin45^o=(7)/(h)`

Solving for h

`\displaystyle h=(7)/(sin45^o)=(7)/((√(2))/(2))=(14)/(√(2))`

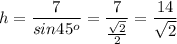
Rationalizing

`\displaystyle h=(14)/(√(2))\cdot (√(2))/(√(2))=(14√(2))/(2)=7√(2)`