Answer:
Probability that the calculator works properly for 74 months or more is 0.04 or 4%.
Explanation:
We are given that the life span of a calculator has a normal distribution with a mean of 60 months and a standard deviation of 8 months.
Firstly, Let X = life span of a calculator
The z score probability distribution for is given by;
Z =
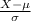 ~ N(0,1)
~ N(0,1)
where,
 = population mean = 60 months
= population mean = 60 months
 = standard deviation = 8 months
= standard deviation = 8 months
Probability that the calculator works properly for 74 months or more is given by = P(X
 74 months)
74 months)
P(X
 74) = P(
74) = P(
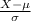

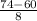 ) = P(Z
) = P(Z
 1.75) = 1 - P(Z < 1.75)
1.75) = 1 - P(Z < 1.75)
= 1 - 0.95994 = 0.04
Therefore, probability that the calculator works properly for 74 months or more is 0.04 or 4%.