Step-by-step explanation:
The given data is as follows.
Radius of the sphere (R) = 10 cm = 0.01 m (as 1 m = 100 cm)
Distance from the center (r) = 4 cm = 0.04 m
Charge density (
 ) = 100
) = 100
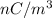
=
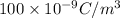 (As 1 nm =
(As 1 nm =
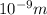 )
)
As the relation between charge and potential difference is as follows.
Q =

=
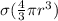
=
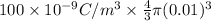
=
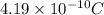
Expression for electric field is as follows.
E(r) =
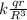
Electric potential, V(r) =
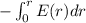
=
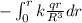
=

=
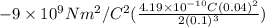
= -3 V
Thus, we can conclude that the magnitude of the potential difference between the center and a point 4.0 cm away is -3 V.