Question

A car is stopped at an entrance ramp to a freeway; its driver is preparing to merge. At a certain moment while stopped, this driver observes a platoon of vehicles a distance x0 upstream and initiates the merge maneuver. The platoon approaches the entrance ramp at a constant speed v. The stopped car can accelerate from speed 0 to v at uniform acceleration rate a .

Find the latest time at which the stopped car can safely start the merge maneuver; i.e., derive an expression for the "latest safe start time" in terms of the variables x0, v and a. Assume this latest time enables the platoon to maintain its constant speed and "just touch" the merging car's trajectory. Ignore the physical dimensions of the car.

Answer 1

T =
`\sqrt{(2X_(0) )/(a) }`

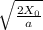
Step-by-step explanation:

Given,

Initial Velocity, u=0

As platoon is moving with constant velocity v,

Final Velocity, v=v

The vehicle starts from 0 to v at constant acceleration of a,

Relevent expressions:

v=u+at...........................(1)

v2=u2+2as.....................(2)

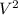`V^(2)` = 2aS, as S =
`X_(0)`,

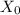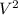`V^(2)` = 2a
`X_(0)`,

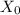From(1)

v=at

Hence

(at)^2=2a
`X_(0)`

`T^(2)` =
`(2aX_0)/(a^(2) )`

T =
`\sqrt{(2X_(0) )/(a) }`

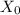
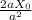
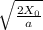
This is the final expression for time.