Question

A cardboard box without a lid is to have a volume of 10,976 cm3. Find the dimensions that minimize the amount of cardboard used. (Let x, y, and z be the dimensions of the cardboard box.)

Answer 1

28cm*28cm*14cm

Explanation:

Five side box for cardboard are: xy, 2xz and 2yz

so the function of Area will be:

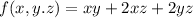`f(x,y.z)=xy+2xz+2yz` equation 1

The Volume will be:

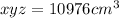`xyz=10976 cm^(3)` equation 2

we can make z the subject of the formula by divide both side by xy

now z =
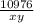`(10976)/(xy)` equation 3

To eliminate z, substitute z into equation 1

f(x,y)=xy+2x
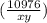`((10976)/(xy))`+2y

f(x,y)=xy+
`(21952)/(y)`+
`(21952)/(x)`

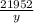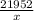
Now we have to derivative of x and y

`f_(x)= y-(21952)/(x^(2) )`

`f_(y)=x-(21952)/(y^(2) )`

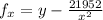
for y and x

`y-(21952)/(x^(2) ) =0\\y=21952x^(-2) \\x-(21952)/(y^(2) ) =0\\x=21952y^(-2)`

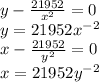
substitute y into x

`x=21952(21952x^(-2) )^(-2) \\x=(21952)^(-1) x^(4) \\ x^(3) =21952\\cube-root-both side\\x=\sqrt[3]{21952} \\x=28`

to find y

`y=21952(28)^(-2) \\y=28`

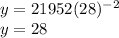
to find z

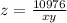
`z=(10976)/(xy)`

z=
`(10976)/(28*28)`

`z=14`

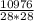
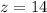
so The dimensions are 28cm*28cm*14cm