Question

A Broadway theater has 800 ​seats, divided into​ orchestra, main, and balcony seating. Orchestra seats sell for $ 50, main seats for $ 40 , and balcony seats for $ 25.  If all the seats are​ sold, the gross revenue to the theater is $ 30 comma 150.  If all the main and balcony seats are​ sold, but only half the orchestra seats are​ sold, the gross revenue is $ 26, 150. How many are there of each kind of​ seat?

Answer 1

Explanation:

Let's represent the number of orchestra seats with the variable
`o`, the number of main seats with the variable
`m`, and the number of balcony seats with the variable
`b`.

From the first sentence, we know that the total number of seats shared among these three sections is 800, so we can setup the following equation:

`o + m + b = 800`

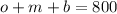
From the second sentence, we can setup an equation for the total revenue by seat type as follows:

`50o + 40m + 25b = 30150`

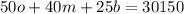
From the third sentence, we know that we cut the number of orchestra seats in half, and the revenue goes from $30150 to $26150, a difference of $4000. Since we know each orchestra seat is $50, we can divide
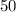`50` into
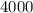`4000` to determine there are
`80` orchestra seats, but remember, this number is HALF the total seats available, so there are
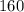`160` total orchestra seats.

We can now plug in
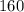`160` for
`o` in the two equations above:

`160 + m + b = 800`

`m + b = 640`

`50(160) + 40m + 25b = 30150`

`8000 + 40m + 25b = 22150`

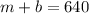
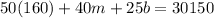
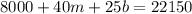
Now we can solve one for
`m` in the first equation and plug it into the second equation:

`m = 640 - b`

`40(640 - b) + 25b = 22150`

`25600 - 40b + 25b = 22150`

`-15b = -3450`

`b = 230`

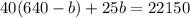
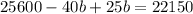
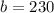
We know know there are
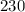`230` balcony seats. Finally, we can plug this number into our original equation to get the number of main seats:

`m + 230 = 640`

`m = 410`

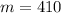
So there are 160 orchestra seats, 410 main seats, and 230 balcony seats.