Answer:
Probability that a car can complete the transaction in less than 5 minutes is 0.465.
Explanation:
We are given that the manager of a gas station has observed that the times required by drivers to fill their car's tank and pay are quite variable. In fact, the times are exponentially distributed with a mean of 8 minutes.
Let X = times required by drivers to fill their car's tank and pay
The probability distribution function of exponential distribution is given by;
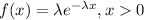 where,
where,
 = parameter of distribution.
= parameter of distribution.
Now, the mean of exponential distribution is =
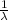 which is given to us as 8 minutes that means
which is given to us as 8 minutes that means
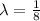 .
.
So, X ~ Exp(
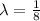 )
)
Also, we know that Cumulative distribution function (CDF) of Exponential distribution is given as;
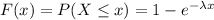 , x > 0
, x > 0
Now, Probability that a car can complete the transaction in less than 5 minutes is given by = P(X < 5 min)
P(X < 5 min) =
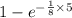 {Using CDF}
{Using CDF}
= 1 - 0.5353 = 0.465
Therefore, probability that a car can complete the transaction in less than 5 minutes is 0.465.