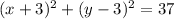Question

Find the equation of a circle that has a diameter with the endpoints given by the points A(-4,9) and B (- 2, - 3) )

Answer 1

The equation of the circle is
`(x+3)^(2)+(y-3)^(2)=37`

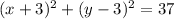
Step-by-step explanation:

Given that the endpoints of the circle are A(-4,9) and B(-2,-3)

We need to determine the equation of the circle.

Center:

The center of the circle can be determined using the midpoint formula,

`Center=((x_1+x_2)/(2), (y_1+y_2)/(2))`

Substituting the coordinates A(-4,9) and B(-2,-3), we get,

`Center=((-4-2)/(2),(9-3)/(2))`

`Center=((-6)/(2),(6)/(2))`

`Center=(-3,3)`

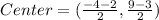
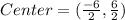
Thus, the center of the circle is (-3,3)

Radius:

The radius of the circle can be determined using the distance formula,

`r=\sqrt{\left(x_(2)-x_(1)\right)^(2)+\left(y_(2)-y_(1)\right)^(2)}`

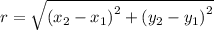
Substituting the center (-3,3) and the endpoint (-4,9), we get,

`r=\sqrt{\left(-4+3\right)^(2)+\left(9-3\right)^(2)}`

`r=\sqrt{\left(-1\right)^(2)+\left(6\right)^(2)}`

`r=√(1+36)`

`r=√(37)`

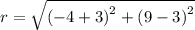
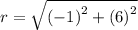
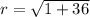
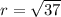
Thus, the radius of the circle is
`√(37)`

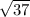
Equation of the circle:

The standard form of the equation of the circle is given by

`(x-a)^(2)+(y-b)^(2)=r^(2)`

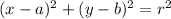
where (a,b) is the center and r is the radius.

Substituting the values, we have,

`(x+3)^(2)+(y-3)^(2)=(√(37))^(2)`

`(x+3)^(2)+(y-3)^(2)=37`

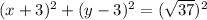
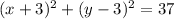
Thus, the equation of the circle is
`(x+3)^(2)+(y-3)^(2)=37`