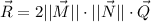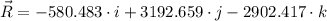Answer:
a)
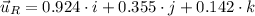 , b)
, b)
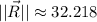 , c)
, c)
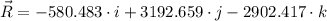
Step-by-step explanation:
a) The resultant vector is obtained by summing all components:
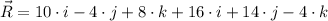
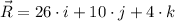
Its magnitude is determined herein:
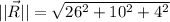
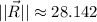
Unit vector in the given direction is:
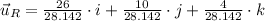
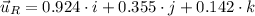
b) The resultant vector is obtained by summing all components:
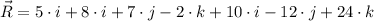
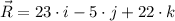
Its magnitude is determined herein:
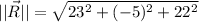
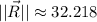
c) Magnitudes of
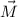 and
and
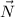 are, respectively:
are, respectively:
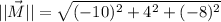
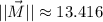
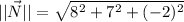
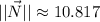
The sum of both vectors is:
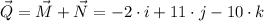
Finally, the resultant is: