Question

Christine has always been weak in mathematics. Based on her performance prior to the final exam in Calculus, there is a 51% chance that she will fail the course if she does not have someone to coach her. With a coach, her probability of failing decreases to 21%. There is only a 61% chance that she will find someone at such short notice.

a. What is the probability that Christine fails the course? (Round your answer to 4 decimal places.)

b. Christine ends up failing the course. What is the probability that she had found someone to help? (Round your answer to 4 decimal places.)

Answer 1

a) 0.3270 = 32.70% probability that Christine fails the course

b) 0.3917 = 39.17% probability that she had found someone to help

Explanation:

We have these following probabilities:

61% probability that Christine find a coach.

100 - 61 = 39% probability that Christine does not find a coach.

With a coach, a 21% probability of failing.

Without a coach, a 51% probability of failing.

a. What is the probability that Christine fails the course?

21% of 61%(finds a tutor) plus 51% of 39%(does not find a tutor). So

P = 0.21*0.61 + 0.51*0.39 = 0.327.

0.327 = 32.7% probability that Christine fails the course

b. Christine ends up failing the course. What is the probability that she had found someone to help?

This can be formulated by the Bayes formula:

`P(B|A) = (P(B)*P(A|B))/(P(A))`

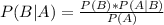
In which P(B|A) is the probability of B happening given that A happened and P(A|B) is the probability of A happening given that B happened.

In this question.

P(B|A) is the probability of finding a tutor given that she failed.

P(B) is the probability of finding a tutor. So P(B) = 0.61.

P(A|B) is the probability of failing when finding a tutor. So P(A|B) = 0.21

P(A) is the probability of failing. So P(A) = 0.327.

So

`P(B|A) = (P(B)*P(A|B))/(P(A)) = (0.61*0.21)/(0.327) = 0.3917`

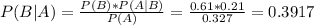
0.3917 = 39.17% probability that she had found someone to help