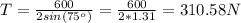Question

A gymnast of mass mb suspends himself on the rings with his body upright and straight arms that are horizontal with which he clutches the rings. Each ring is suspended by a rope with tension T that makes an acute angle d with his arms, and the rings are separated by a distance d.

a. Solve for the T and d. Assume symmetry.

b. If the gymnast weighs 600 N, d = 75 degrees, and d = 1.8 m, find T

Answer 1

a.
`T = (mg)/(2sin(d))`

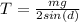
b. 310.58 N on each rope

Step-by-step explanation:

a. Since the system is symmetrical, tension forces on both ropes are the same. So the T (tension) force can be split in to 2 components: the horizontal forces (of the 2 ropes) are equal and opposite to each other and thus cancel out themselves. The vertical forces are in the opposite direction with the gymnast gravity and equal in magnitude

The vertical component is
`2Tsin(d) = mg`

`T = (mg)/(2sin(d))`

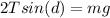
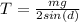
Where d here is the acute angle between the rope and the horizontal arms.

The distance d between the rings are the total arm lengths of the gymnast

b.
`T = (600)/(2sin(75^o)) = (600)/(2*1.31) = 310.58 N`