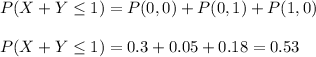Question

When an automobile is stopped with a roving safety patrol,each tire is checked for tire wear, and each headlight is checkedto see whether it is properly aimed. Let X denote the numberof headlights that need adjustment, and let Y denote the numberof defective tires.

a) if X and Y are independent with Px(0) = .5, Px(1) =.3,Px(2) =.2 and Py(0) =.6, Py(1) =.1, Px(2) =Py(3) =..05, Py(4) =.2,display the joint probability distribution table.
b) compute P(X<= 1 and Y <= 1) fromthe joint probability distribution table and verify that it isequals to the product P(X <= 1) * P(Y<=1)
c) What is P(X+Y = 0) (theprobability of no violations)?
d) Compute P(X + Y <= 1).

Answer 1

a) Joint ptobability distribution

`\begin{pmatrix} &Y=0&Y=1&Y=2&Y=3&Y=4\\X=0&0.3&0.05&0.025&0.025&0.1\\ X=1&0.18&0.03&0.015&0.015&0.06 \\ X=2&0.12&0.02&0.01&0.01&0.04\end{pmatrix}`

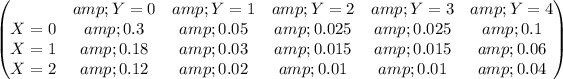
b) P(X<= 1 and Y <= 1) = P(X<= 1) * P(Y<=1) = 0.56

c) P(X + Y = 0)=0.3

d) P(X + Y <= 1)=0.53

Explanation:

We have to construct the joint probability table with the marginal probabilities of X and Y.

X can take values from 0 to 2, and Y can take values from 0 to 4.

We can calculate each point of the joint probability as:

`P(x,y)=P_x(x)*P_y(y)`

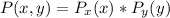
Then, the joint probabilities are:

X=0 Y=0 Px=0.5 Px=0.6 P(0,0)=0.3

X=0 Y=1 Px=0.5 Px=0.1 P(0,1)=0.05

X=0 Y=2 Px=0.5 Px=0.05 P(0,2)=0.025

X=0 Y=3 Px=0.5 Px=0.05 P(0,3)=0.025

X=0 Y=4 Px=0.5 Px=0.2 P(0,4)=0.1

X=1 Y=0 Px=0.3 Px=0.6 P(1,0)=0.18

X=1 Y=1 Px=0.3 Px=0.1 P(1,1)=0.03

X=1 Y=2 Px=0.3 Px=0.05 P(1,2)=0.015

X=1 Y=3 Px=0.3 Px=0.05 P(1,3)=0.015

X=1 Y=4 Px=0.3 Px=0.2 P(1,4)=0.06

X=2 Y=0 Px=0.2 Px=0.6 P(2,0)=0.12

X=2 Y=1 Px=0.2 Px=0.1 P(2,1)=0.02

X=2 Y=2 Px=0.2 Px=0.05 P(2,2)=0.01

X=2 Y=3 Px=0.2 Px=0.05 P(2,3)=0.01

X=2 Y=4 Px=0.2 Px=0.2 P(2,4)=0.04

We can write it in the form of a matrix:

`\begin{pmatrix} &Y=0&Y=1&Y=2&Y=3&Y=4\\X=0&0.3&0.05&0.025&0.025&0.1\\ X=1&0.18&0.03&0.015&0.015&0.06 \\ X=2&0.12&0.02&0.01&0.01&0.04\end{pmatrix}`

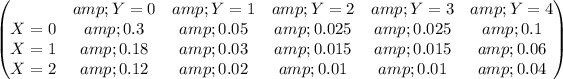
b) From the joint probability P(X<= 1 and Y <= 1) is equal to

`P(X\leq 1 \& Y \leq 1)=P(0,0)+P(0,1)+P(1,0)+P(1,1)\\\\P(X\leq 1 \& Y \leq 1)=0.3+0.05+0.18+0.03=0.56`

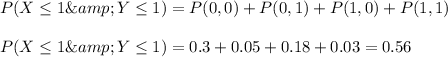
We can calculate P(X<= 1) * P(Y<=1)

`P_x(X\leq 1)=P_x(0)+P_x(1)=0.5+0.3=0.8\\\\P_y(Y\leq1)=P_y(0)+P_y(1)=0.6+0.1=0.7\\\\P_x(X\leq1)*P_y(Y\leq1)=0.8*0.7=0.56`

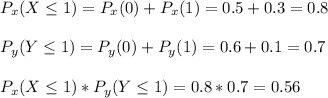
Both calculations give the same result.

c) Probability of no violations

`P(X+Y=0)=P(0,0)=0.3`

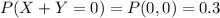
d) P(X + Y <= 1)

`P(X+Y \leq 1)=P(0,0)+P(0,1)+P(1,0)\\\\P(X+Y \leq 1)=0.3+0.05+0.18=0.53`