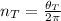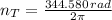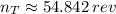Answer:
a)
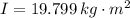 , b)
, b)
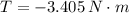 , c)
, c)
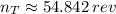
Step-by-step explanation:
a) The net torque is:
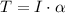
Let assume a constant angular acceleration, which is:
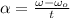

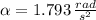
The moment of inertia of the wheel is:

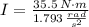
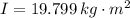
b) The deceleration of the wheel is due to the friction force. The deceleration is:
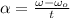
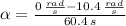
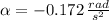
The magnitude of the torque due to friction:

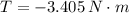
c) The total angular displacement is:
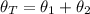
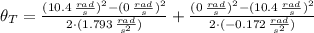
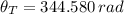
The total number of revolutions of the wheel is: