Question

If r= 11 units and x = 14 units, then what is the volume of the cylinder

Answer 1

`1694 \pi`

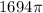
Explanation:

I don't see a diagram, so I'm assuming that r is the radius and x is the height of a right circular cylinder (like a soup can).

The volume of the cylinder can be found from the formula

`V=\pi (\text{radius})^2 \cdot (\text{height})`

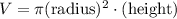
using the variables in your problem, this is

`V=\pi r^2x`

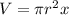
Plug in the given values for r and x.

`V=\pi(11)^2(14) \\ V=\pi(121)(14) \\ V=1694\pi`

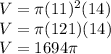
If you need an approximate decimal value for the volume, use a value of pi (ask your teacher how accurate it should be).

Example: Using pi = 3.1416,

`V \approx (1694)(3.1416)=5321.8704`

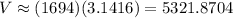
You might be asked to round that answer, say to 5322 cubic units.