Question

First, you will investigate purely vertical motion. The kinematics equation for vertical motion (ignoring air resistance) is given by y(t)=y0+v0t−(1/2)gt2 , where y0=0 is the initial position, v0 is the initial speed, and g is the acceleration due to gravity. Drag the cannon downwards so it is at ground level, or 0 m (which represents the initial height of the object), then fire the pumpkin straight upward (at an angle of 90∘) with an initial speed of 14 m/s . How long does it take for the pumpkin to hit the ground?

Answer 1

Answer: It takes 2.85 seconds.

Explanation: according to the question, the kinematics equation for vertical motion is

`y(t) = y_(0) + v_(0) .t - (1)/(2) .gt^(2)`

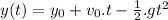
y₀ is the initial postion and equals 0 because it is fired at ground level;

v₀ is the initial speed and eqauls 14m/s;

g is gravity and it is 9.8m/s²;

y(t) is the final position and equals 0 because it is when the pumpkin hits the ground;

Rewriting the equation, we have:

0 + 14t -
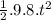`(1)/(2).9.8.t^(2)` = 0

14t - 4.9t² = 0

t(14 - 4.9t) = 0

For this equation to be zero,

t = 0 or

14 - 4.9t = 0

- 4.9t = - 14

t =
`(14)/(4.9)`

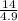
t = 2.86

It takes 2.86 seconds for the pumpkin to hit the ground.