Question

Xavier invested $20,000 in an account paying an interest rate of 9\frac{3}{4}9 4 3 ​ % compounded continuously. Samantha invested $20,000 in an account paying an interest rate of 9\frac{3}{8}9 8 3 ​ % compounded daily. To the nearest hundredth of a year, how much longer would it take for Samantha's money to double than for Xavier's money to double?

Answer 1

0.29 years

Step-by-step explanation:

Answer 2

Answer: It will take Samantha's money 102 more days to double than it would take Xavier's money

Step-by-step explanation:

We will put down the continuous compounding formula in order to find the number of years it will take for Xavier's money to double.

`Fv = Pv* ( e^(i*t) )`

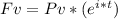
Fv = future value (40,000), Pv = present value (20,000), e = mathematical constant (2.7183), i = interest (
`9(3)/(4)` or 39/4% or 9.75% or 0.0975), t = time in years (the unknown).

Substituting appropriately:-

40,000 = 20,000 × [
`2.7183^(0.0975*t)`]

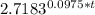2.7183^0.0975t = 40000/20000

2.7183^0.0975t = 2

0.0975t =
`(log2_(10) )/(log2.7183_(10) )`

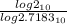
0.0975t = 0.69314

t = 0.69314/0.0975

t = 7.11 years

Therefore, it will take 7.11 years for Xavier's initial deposit to double, if it is compounded continuously at that rate.

On the other hand, Samantha invested same amount as Xavier but the account pays an interest of
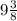`9(3)/(8)`% compounded daily.

In order to calculate the number of years it will take Samantha's initial deposit to double we need to put down the formula for calculating compound interest:-

Fv = Pv × (1 +(r/n))^(n×t)

Where Fv = future value ($40,000), Pv = present value ($20,000), r = rate =

(
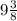`9(3)/(8)`% or 75/8% or 9.375% or 0.09375), n = the number of times it is compounded in a year ( it is 365 this time since it's compounded daily), t = the number of years (the unknown).

Substituting accordingly:-

40,000 = 20,000 × [
`(1+(0.09375)/(365) )^(365*t)`]

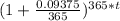40,000 = 20,000×[(1+0.00025685)^365t]

40,000 = 20,000 × [1.00025685]^365t

1.00025685^365t = 40,000/20,000

`1.00025685^(365t) = 2`

365t =
`(log2_(10) )/(log1.00025685_(10) )`

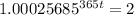
365t = 2699

t = 2699/365

t = 7.39 years

It will take 7.39 years for Samantha's initial deposit to double, if it is compounded daily at this rate.

Now, Xavier's money compounded continuously will double in 7.11 years and Samantha's initial deposit will double in 7.39 years if compounded daily.

The difference in the periods it will take for the sums to double the initial deposits is 7.39 - 7.11 years = 0.28 years.

To convert this to days, we will simply multiply 0.28 by 365

i.e 0.28 years × 365 days = 102 days.

This means that it will take Samantha's money 102 more days to double than it would take Xavier's.