Question

Early one October, you go to a pumpkin patch to select your Halloween pumpkin. You lift the 2.9 kg pumpkin to a height of 1.5 m , then carry it 50.0 m (on level ground) to the check-out stand.What is the work you do on the pumpkin as you lift it from the ground and how much work do you do on the pumpkin as you carry it from the field?

Answer 1

Work done in lifting to a height of 1.5 m is 42.63 J.

Work done in carrying it to 50 m is 0 J

Step-by-step explanation:

Given:

Mass of the pumpkin (m) = 2.9 kg

Vertical displacement of the pumpkin (y) = 1.5 m

Horizontal displacement of the pumpkin (x) = 50 m

Acceleration due to gravity (g) = 9.8 m/s²

Work done by a force is given by the formula:

`W=FS\cos\theta`

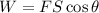
Where,

`F\to force\ applied\\\\S\to displacement\ caused\\\\\theta\to angle\ between\ F\ and\ S`

• Now, the work done is maximum when both force and displacement is in same direction. (
  `\theta=0^\circ`)
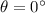• Work done is minimum when both force and displacement are in opposite direction. (
  `\theta=180^\circ`)
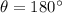• Work done is zero when force and displacement are perpendicular to each other. (
  `\theta=90^\circ`)

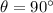Here, as the pumpkin is raised to a height 'h', there is force applied against gravity in the upward direction. So, force and displacement are in same direction and thus the angle is 0° between the force and displacement vectors.

So, work done is given as:

`W=Force* Vertical\ displacement`

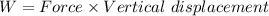
Force applied is equal to the gravitational force applied by the Earth but in the opposite direction.

So, Force = mg =
`2.9* 9.8 = 28.42\ N`

So, work,
`W=Fy=28.42* 1.5=42.63\ J`

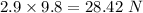
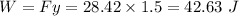
So, work done in lifting the pumpkin is 42.63 J.

Now, when the pumpkin is carried to the check-out stand, the displacement is horizontal while the force applied is still in the upward direction.

So, the force and displacement are perpendicular to each other. Thus, the work done is zero.