Question

Find the average rate of change of f(x) = x + 6 on [4,9]. Round your answer to the nearest hundredth.

Answer 1

0.14

Explanation:

i be smart

Answer 2

The average rate of change of f(x) = x + 6 on [4,9] is 1.

Explanation:

Given a function y, the average rate of change S of y=f(x) in an interval
`(x_(s), x_(f))` will be given by the following equation:

`S = (f(x_(f)) - f(x_(s)))/(x_(f) - x_(s))`

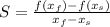
In this problem, we have that:

`f(x) = x + 6`

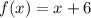
Interval [4,9]. So

`x_(s) = 4, x_(f) = 9, f(x_(f)) = f(9) = 9+6 = 15, f(x_(s)) = f(4) = 4+6 = 10`

`S = (f(x_(f)) - f(x_(s)))/(x_(f) - x_(s)) = (15 - 10)/(9 - 4) = 1`

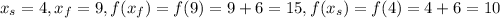
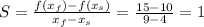
The average rate of change of f(x) = x + 6 on [4,9] is 1.