Question

Particle P in the metal sheet preforms simple harmonic oscillations. When the displacement of P is 3.2cm, the magnitude of its restoring force is 7.9 m/s^2. Calculate the magnitude of the net restoring force on P when it's displacement is 2.3cm

Answer 1

The magnitude of the restoring force per unit mass is 5.175 m/s².

Step-by-step explanation:

To solve the question, we note that from Hooke's law

F = -k·x

Where:

F = Restoring force

k = Constant of restoration and

x = Displacement of the particle

Therefore when we have, F = m × a, this gives

m × a = -k·x or

a =
`-(k)/(m) * x`

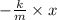
That is the restoring force per unit mass is given by;

a =
`-(k)/(m) * x`

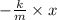
Where:

a = Acceleration

m = mass of the object.

For a given mass,
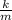`(k)/(m)` is also constant

Therefore, when a = 7.9 m/s²

x = 3.2 cm = , we have

a =
`-(k)/(m) * x` → 7.9 m/s² =
`-(k)/(m)` × ‪0.032‬ m or

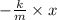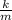`(k)/(m)` = (7.9 m/s²)/(0.032‬ m ) = 225

Therefore when x = 2.30 cm = 0.023, we have

a =
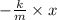`-(k)/(m) * x` = 225×0.023 m = 5.175 m/s²

The restoring force per unit mass = 5.175 m/s².