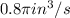Question

A Coffee Pot A coffee pot in the form of a circular cylinder of radius 2 in. is being filled with water flowing at a constant rate. If the water level is rising at the rate of 0.2 in./s, what is the rate (in in3/s) at which water is flowing into the coffee pot?

Answer 1

`0.8\pi in^3/s`

Explanation:

We are given that

Radius of cylinder,r=2 in

dh/dt=0.2 in/s

We have to find the rat at which water is flowing into the coffee pot

We know that

Volume of cylinder=
`V=\pi r^2 h`

`(dV)/(dt)=\pi(r^2 (dh)/(dt)+2rh(dr)/(dt))`

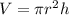
dr/dt=0

Substitute the values

`(dV)/(dt)=\pi ((2)^2* 0.2+0)=0.8\pi in^3/s`

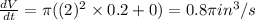
Hence, the rate at which water is flowing into the coffee pot=
`0.8\pi in^3/s`