Question

A university found that of its students withdraw without completing the introductory statistics course. Assume that students registered for the course. a. Compute the probability that or fewer will withdraw (to 4 decimals). b. Compute the probability that exactly will withdraw (to 4 decimals). c. Compute the probability that more than will withdraw (to 4 decimals). d. Compute the expected number of withdrawals.

Answer 1

A university found that 30% of its students withdraw without completing the introductory statistics course. Assume that 20 students registered for the course.

a. Compute the probability that 2 or fewer will withdraw (to 4 decimals).

= 0.0355

b. Compute the probability that exactly 4 will withdraw (to 4 decimals).

= 0.1304

c. Compute the probability that more than 3 will withdraw (to 4 decimals).

= 0.8929

d. Compute the expected number of withdrawals.

= 6

Explanation:

This is a binomial problem and the formula for binomial is:

`P(X = x) = nCx p^(x) q^(n - x)`

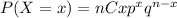
a) Compute the probability that 2 or fewer will withdraw

First we need to determine, given 2 students from the 20. Which is the probability of those 2 to withdraw and all others to complete the course. This is given by:

`P(X = x) = nCx p^(x) q^(n - x)\\P(X = 2) = 20C2(0.3)^2(0.7)^(18)\\P(X = 2) =190 * 0.09 * 0.001628413597\\P(X = 2) = 0.027845872524`

`P(X = x) = nCx p^(x) q^(n - x)\\P(X = 1) = 20C1(0.3)^1(0.7)^(19)\\P(X = 1) =20 * 0.3 * 0.001139889518\\P(X = 1) = 0.006839337111`

`P(X = x) = nCx p^(x) q^(n - x)\\P(X = 0) = 20C0(0.3)^0(0.7)^(20)\\P(X = 0) =1 * 1 * 0.000797922662\\P(X = 0) = 0.000797922662`

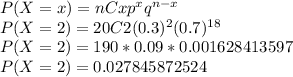
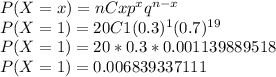
Finally, the probability that 2 or fewer students will withdraw is

`P(X = 2) + P(X = 1) + P(X = 0) \\= 0.027845872524 + 0.006839337111 + 0.000797922662\\= 0.035483132297\\= 0.0355`

b) Compute the probability that exactly 4 will withdraw.

`P(X = x) = nCx p^(x) q^(n - x)\\P(X = 4) = 20C4(0.3)^4(0.7)^(16)\\P(X = 4) = 4845 * 0.0081 * 0.003323293056\\P(X = 4) = 0.130420974373\\P(X = 4) = 0.1304`

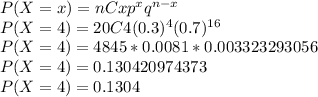
c) Compute the probability that more than 3 will withdraw

First we will compute the probability that exactly 3 students withdraw, which is given by

`P(X = x) = nCx p^(x) q^(n - x)\\P(X = 3) = 20C3(0.3)^3(0.7)^(17)\\P(X = 3) = 1140 * 0.027 * 0.002326305139\\P(X = 3) = 0.071603672205\\P(X = 3) = 0.0716`

Then, using a) we have that the probability that 3 or fewer students withdraw is 0.0355+0.0716=0.1071. Therefore the probability that more than 3 will withdraw is 1 - 0.1071=0.8929

d) Compute the expected number of withdrawals.

E(X) = 3/10 * 20 = 6

Expected number of withdrawals is the 30% of 20 which is 6.