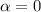Answer:
The angular acceleration is zero
Step-by-step explanation:
When an object is in rotational motion, it has a certain angular velocity, which is the rate of displacement of its angular position.
This angular velocity can change or remain constant - this is given by the angular acceleration, which is:

where
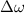 is the change in angular velocity
is the change in angular velocity
 is the time elapsed
is the time elapsed
Therefore, the angular acceleration is the rate of change of angular velocity.
In this problem, the bicycle rotates at a constant angular velocity of
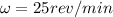
This means that the change in angular velocity is zero:
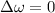
And so, that the angular acceleration is zero: