Question

An aluminum wire 1.628 mm in diameter (14-gauge) carries a current of 3.00 amps. (a) What is the absolute value of the charge density (concentration of moving charged particles) in the wire? (b) What is the drift velocity of the electrons? (c) What would be the drift velocity if the same gauge copper were used instead of aluminum? The density of copper is 8.96 g/cm3 and the density of aluminum is 2.70 g/cm3. The molar mass of aluminum is 26.98 g/mol and the molar mass of copper is 63.5 g/mol. Assume each atom of metal contributes one free electron.

Answer 1

Step-by-step explanation:

(a). First of all, we calculate the number of atoms per cm^{3}, and by taking into account that each atom contributes with one free electron we have

`n=(\rho N_(A))/(M)=(8.96(g)/(cm^(3))*6.023*10^(23)(atm)/(mol))/(63.5(g)/(mol))=8.49*10^(22)(atm)/(cm^(3))`
`\rho=n|e|=(6.02*10^(22)(atm)/(cm^(3)))(1.6*10^(-19)C)=96320(C)/(cm^(3))`

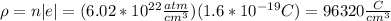
(b)

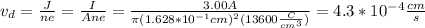
`v_(d)=(J)/(ne)=(I)/(Ane)=(3.00A)/(\pi (1.628*10^(-1)cm)^(2)(13600(C)/(cm^(3))))=4.3*10^(-4)(cm)/(s)`

(c)

`n=(\rho N_(A))/(M)=(2.70(g)/(cm^(3))*6.023*10^(23)(atm)/(mol))/(26.98(g)/(mol))=6.02*10^(22)(atm)/(cm^(3))`

`\rho=n|e|=(8.49*10^(22)(atm)/(cm^(3)))(1.6*10^(-19)C)=13600(C)/(cm^(3))`

`v_(d)=(J)/(ne)=(I)/(Ane)=(3.00A)/(\pi (1.628*10^(-1)cm)^(2)(96320(C)/(cm^(3))))=6.08*10^(-5)(cm)/(s)`

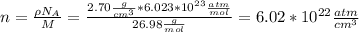
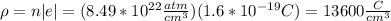
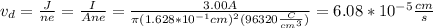
I hope this is useful for you

P.D please change 1.628 (the diameter) by 0.814(the radius) in the calculation

:)