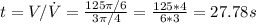Question

A spherical hot-air balloon is initially filled with air at 120 kPa and 20°C with an initial diameter of 5 m. Air enters this balloon at 120 kPa and 20°C with a velocity of 3 m/s through a 1-m-diameter opening. How many minutes will it take to inflate this balloon to a 16.9-m diameter when the pressure and temperature of the air in the balloon remain the same as the air entering the balloon? The gas constant of air is R = 0.287 kPa·m3/kg·K.

Answer 1

27.78 s

Step-by-step explanation:

Assume ideal gas, since pressure and temperature of the air inside the balloon is the same as air entering the balloon, then the volume (and its rate) stays the same.

The cross-sectional area of the hole where air enters

`A = \pi d^2/4 = \pi 1^2/4 = \pi/4 m^2`

Hence the volume rate:

`\dot{V} = vA = 3*\pi/4 = 3\pi/4 m^3/s`

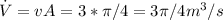
The total volume of the spherical balloon is

`V = 4\pi r^3/3 = 4\pi (5/2)^3/3 = 125\pi/6 m^3`

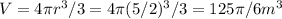
Hence the time it takes to fill this much at a constant rate of 3π/4 is

`t = V/\dot{V} = (125\pi/6)/(3\pi/4) = (125*4)/(6*3) = 27.78 s`