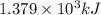Answer: The Gibbs free energy of the given reaction is
Step-by-step explanation:
The equation used to calculate Gibbs free energy change is of a reaction is:
![\Delta G^o_(rxn)=\sum [n* \Delta G^o_f_((product))]-\sum [n* \Delta G^o_f_((reactant))]](https://img.qammunity.org/2021/formulas/chemistry/college/pjnn8zvfjt8lvu7mr2f656y7nnmawajipo.png)
For the given chemical reaction:
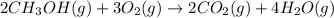
The equation for the Gibbs free energy change of the above reaction is:
![\Delta G^o_(rxn)=[(2* \Delta G^o_f_((CO_2(g))))+(4* \Delta G^o_f_((H_2O(g))))]-[(2* \Delta G^o_f_((CH_3OH(g))))+(3* \Delta G^o_f_((O_2(g))))]](https://img.qammunity.org/2021/formulas/chemistry/college/o460x797fd5apw34ptimgwtse6m1d26was.png)
We are given:
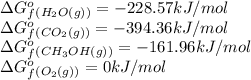
Putting values in above equation, we get:
![\Delta G^o_(rxn)=[(2* (-394.36))+(4* (-228.57))]-[(2* (-161.96))+(3* (0))]\\\\\Delta G^o_(rxn)=-1379.08kJ/mol](https://img.qammunity.org/2021/formulas/chemistry/college/z4rqwfwpaepu8ceqiaed61nkzbn6y9xzin.png)
The equation used to Gibbs free energy of the reaction follows:
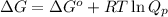
where,
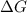 = free energy of the reaction
= free energy of the reaction
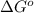 = standard Gibbs free energy = -1379.08 kJ/mol = -1379080 J/mol (Conversion factor: 1 kJ = 1000 J)
= standard Gibbs free energy = -1379.08 kJ/mol = -1379080 J/mol (Conversion factor: 1 kJ = 1000 J)
R = Gas constant = 8.314 J/K mol
T = Temperature =
![25^oC=[273+25]K=298K](https://img.qammunity.org/2021/formulas/chemistry/college/xuv7m8qes7ftb60bgj8ln796iseb65owra.png)
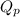 = Ratio of concentration of products and reactants =
= Ratio of concentration of products and reactants =
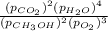
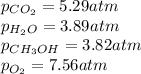
Putting values in above expression, we get:
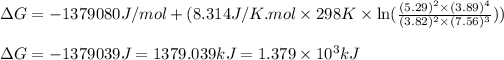
Hence, the Gibbs free energy of the given reaction is