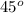Question

A light ray in air strikes a glass plate whose index of refraction is 1.42. Some of the light reflects off the surface of the plate, but most of it enters the glass. If the angle of refraction is one-half the angle of reflection, the angle of refraction is closest to which one of the following angles?

a. 41°
b. 43°
c. 37°
d. 45°
e. 39°

Answer 1

E) 39°

Step-by-step explanation:

Answer 2

The angle of refraction is closest to
`45^(o)`

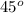
Step-by-step explanation:

Snell's law compares the ratios of the angles of incident and refraction, and it would be applied in solving this problem.

Given the

Refractive index η= 1.42

angle of incident = i

angle of refraction = r = 1/2 x i = i/2

applying Snell's law;

η =
`(sini)/(sin(i)/(2) )`

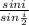
applying trigonometric identity (sin 2x=2sinxcosx )

sin 2i = 2sinicosi

1.42 =
`(2 sin(i/2)cos(i/2))/(sin (i/2) )`

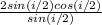
cos i/2 = 1.42/2

cos i/2 = 0.71

i/2 =
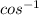`cos^(-1)` 0.71 =
`44.765^(o)`

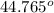
i/2 ≈
`45^(o)`

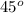
Therefore the angle of refraction is closest to
`45^(o)`