Question

When the magnetic flux through a single loop of wire increases by , an average current of 40 A is induced in the wire. Assuming that the wire has a resistance of , (a) over what period of time did the flux increase? (b) If the current had been only 20 A, how long would the flux increase have taken?

Answer 1

COMPLETE QUESTION:

When the magnetic flux through a single loop of wire increases by 30 Tm^2 , an average current of 40 A is induced in the wire. Assuming that the wire has a resistance of 2.5 ohms , (a) over what period of time did the flux increase? (b) If the current had been only 20 A, how long would the flux increase have taken?

Answer:

(a). The time period is 0.3s.

(b). The time period is 0.6s.

Step-by-step explanation:

Faraday's law says that for one loop of wire the emf
`\varepsilon` is

`(1). \: \: \varepsilon = (\Delta \Phi_B)/(\Delta t )`

and since from Ohm's law

`\varepsilon = IR`,

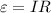then equation (1) becomes

`(2). \: \:IR= (\Delta \Phi_B)/(\Delta t ).`

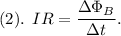
(a).

We are told that the change in magnetic flux is
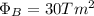`\Phi_B = 30Tm^2`, the current induced is
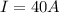`I = 40A`, and the resistance of the wire is
`R = 2.5\Omega`; therefore, equation (2) gives

`(40A)(2.5\Omega)= (30Tm^2)/(\Delta t ),`

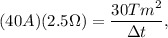
which we solve for
`\Delta t` to get:

`\Delta t = (30Tm^2)/((40A)(2.5\Omega)),`

`\boxed{\Delta t = 0.3s}`,

which is the period of time over which the magnetic flux increased.

(b).

Now, if the current had been
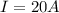`I =20A`, then equation (2) would give

`(20A)(2.5\Omega)= (30Tm^2)/(\Delta t ),`

`\Delta t = (30Tm^2)/((20A)(2.5\Omega)),`

`\boxed{\Delta t = 0.6 s\\}`

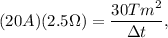
which is a longer time interval than what we got in part a, which is understandable because in part a the rate of change of flux
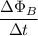`(\Delta \Phi_B)/(\Delta t)` is greater than in part b, and therefore , the current in (a) is greater than in (b).