Question

The thickness of a flange on an aircraft component is uniformly distributed between 0.95 and 1.05 millimeters. (a) Determine the proportion of flanges that exceeds 0.99 millimeters.

Answer 1

The proportion of flanges that exceeds 0.99 millimeters is 0.6

Step-by-step explanation:

Given;

integral range of [0.95, 1.05]

Let X be a variable with uniform distribution over the given range.

`Then, f(x) = (1)/(1.05 -0.95) =10`

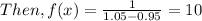
1 - 0.95 = 0.05, 1.05 - 1 = 0.05

`\ minimum, f_(x) = (0.05)/(1.05 -0.95) =0.5\\\\`

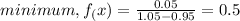
interval = 10 - 0.5 = 9.5

F(x) = 10x + 9.5

When, X exceeds 0.99 millimeters, then the proportion of flanges will be;

P (X > x) = 1 - F(x)

P( X > 0.99 ) = 1 - 10(0.99) + 9.5

P( X > 0.99 ) = 0.6

Therefore, the proportion of flanges that exceeds 0.99 millimeters is 0.6