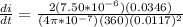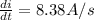Question

A long, thin solenoid has 360 turns per meter and a radius of 1.17 cm. The current in the solenoid is increasing at a uniform rate didt. The magnitude of the induced electric field at a point which is near the center of the solenoid and a distance of 3.46 cm from its axis is 7.50×10−6 V/m.

Calculate di/dt

Answer 1

To solve this problem we will apply the concepts related to the induced voltage or electromotive force. Said force is equivalent to the variation of the magnetic flux over time, and in turn, said flux could be expressed in terms of the cross-sectional area and the magnetic field. Under these relationships and our values we will find the finally desired value.

The induced emf is,

`\int Edl = -(d\phi)/(dt)`

`\int Edl = -((dB)/(dt))A`

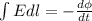
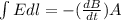
We have:

`B = -\mu_0 ni`

`(dB)/(dt) = -\mu n ((di)/(dt))`

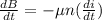
And

`A = \pi r^2`

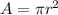
Then

`E (2\pi r) = \mu_0 n ((di)/(dt))(\pi R^2)`

Here,

r = The distance from the axis

R = Radius of the solenoid

Rearrange for
`(di)/(dt)`

`(di)/(dt) = (Er)/(\mu_0nR^2)`

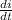
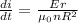
Replacing,

`(di)/(dt) = (2(7.50*10^(-6))(0.0346))/((4\pi*10^(-7))(360)(0.0117)^2)`

`(di)/(dt) = 8.38A/s`