Answer:
Therefore it will take 7.66 hours for 80% of the lead decay.
Step-by-step explanation:
The differential equation for decay is
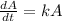
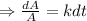
Integrating both sides
ln A= kt+c₁
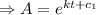
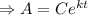 [
[
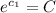 ]
]
The initial condition is A(0)= A₀,
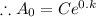

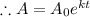 .........(1)
.........(1)
Given that the
 has half life of 3.3 hours.
has half life of 3.3 hours.
For half life
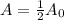 putting this in equation (1)
putting this in equation (1)
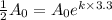
 [taking ln both sides,
[taking ln both sides,
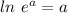 ]
]
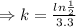
⇒k= - 0.21
Now A₀= 1 gram, 80%=0.8
and A= (1-0.8)A₀ = (0.2×1) gram = 0.2 gram
Now putting the value of k,A and A₀in the equation (1)
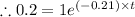
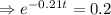

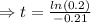
⇒ t≈7.66
Therefore it will take 7.66 hours for 80% of the lead decay.