Question

A manufacturer of Christmas light bulbs knows that 10% of these bulbs are defective. It is known that light bulbs are defective independently. A box of 150 bulbs is selected at random. Answer the following questions. Question 2 (4 points). Find the probability that this box will contain at most 20 defective light bulbs. Show your work or calculator input. (Round your answer to 4 places after the decimal point). Question 3 (2 points): How many defective light bulbs are expected to be found in such boxes, on average? Show your work Question 4 (3 points): Find the standard deviation of defective light bulbs in this case. Show your work. (Round your answer to 2 places after the decimal point).

Answer 1

(a) P(X
`\leq` 20) = 0.9319

(b) Expected number of defective light bulbs = 15

(c) Standard deviation of defective light bulbs = 3.67

Explanation:

We are given that a manufacturer of Christmas light bulbs knows that 10% of these bulbs are defective. It is known that light bulbs are defective independently. A box of 150 bulbs is selected at random.

Firstly, the above situation can be represented through binomial distribution, i.e.;

`P(X=r) = \binom{n}{r} p^(r) (1-p)^(2) ;x=0,1,2,3,....`

where, n = number of samples taken = 150

r = number of success

p = probability of success which in our question is % of bulbs that

are defective, i.e. 10%

Now, we can't calculate the required probability using binomial distribution because here n is very large(n > 30), so we will convert this distribution into normal distribution using continuity correction.

So, Let X = No. of defective bulbs in a box

Mean of X,
`\mu` =
`n * p` =
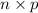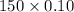`150 * 0.10` = 15

Standard deviation of X,
`\sigma` =
`√(np(1-p))` =
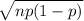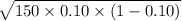`√(150 * 0.10 * (1-0.10))` = 3.7

So, X ~ N(
`\mu = 15, \sigma^(2) = 3.7^(2))`

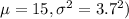
Now, the z score probability distribution is given by;

Z =
`(X-\mu)/(\sigma)` ~ N(0,1)

(a) Probability that this box will contain at most 20 defective light bulbs is given by = P(X
`\leq` 20) = P(X < 20.5) ---- using continuity correction

P(X < 20.5) = P(
`(X-\mu)/(\sigma)` <
`(20.5-15)/(3.7)` ) = P(Z < 1.49) = 0.9319

(b) Expected number of defective light bulbs found in such boxes, on average is given by = E(X) =
`n * p` =
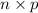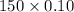`150 * 0.10` = 15.

Standard deviation of defective light bulbs is given by = S.D. =
`√(np(1-p))` =
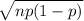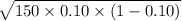`√(150 * 0.10 * (1-0.10))` = 3.67