Question

The population of measurements is approximately normal, with mean 37 cm and standard deviation 5 cm. Suppose that a sample of size 10 is randomly selected from this population. What is the probability that all 10 have a calf circumference greater than 42 cm? Now suppose that a sample of size 10 is randomly selected from the population described in problem 9. What is the probability that the average of the 10 measurements is greater than 42 cm?

Answer 1

a) 0.1587

b) 0.0008

Explanation:

Given that:

Mean (m) = 37 cm

Sample size (n) = 10

standard deviation (s) = 5 cm

a) the z score (z) =
`(x-m)/(s)`

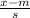
where x = 42 cm

Therefore,
`z=(x-m)/(s)=(42-37)/(5) =1`

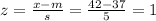
The probability that all 10 have a calf circumference greater than 42 cm =

P(x > 42) = P (z > 1) = 1 - P(z < 1) = 1 - 0.8413 = 0.1587

b) The standard error of the mean is a measure of how far that the sample mean will be from the population mean for a repeated random samples of size n.

The standard error of the mean (e)= s /√n

e = s /(√n ) = 5 / (√10) = 1.5811

The z score (z) =
`(x-m)/(e)`

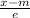
where x = 42 cm

Therefore,
`z=(x-m)/(e)=(42-37)/(1.5811) = 3.16`

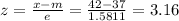
P(x > 42) = P (z > 3.16) = 1 - P(z < 3.16) = 1 - 0.9992 = 0.008