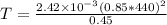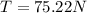Question

A violin string is 45.0 cm long and has a mass of 0.242 g. When tightened on the neck of the violin, the distance between the pin and fret is 42.5 cm. If the string is tightened to play a 'Concert A' of 440. Hz as its fundamental/ first harmonic, what is the tension in the violin string

Answer 1

The tension is 75.22 Newtons

Step-by-step explanation:

The velocity of a wave on a rope is:

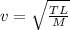`v=\sqrt{(TL)/(M)}` (1)

With T the tension, L the length of the string and M its mass.

Another more general expression for the velocity of a wave is the product of the wavelength (λ) and the frequency (f) of the wave:

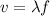`v= \lambda f` (2)

We can equate expression (1) and (2):

`\sqrt{(TL)/(M)}`=
`\lambda f`

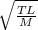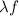
Solving for T

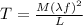`T= (M(\lambda f)^2)/(L)` (3)

For this expression we already know M, f, and L. And indirectly we already know λ too. On a string fixed at its extremes we have standing waves ant the equation of the wavelength in function the number of the harmonic
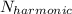`N_(harmonic)` is:

`\lambda_(harmonic)=(2l)/(N_(harmonic))`

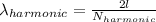
It's is important to note that in our case L the length of the string is different from l the distance between the pin and fret to produce a Concert A, so for the first harmonic:

`\lambda_(1)=(2(0.425m))/(1)=0.85 m`

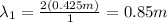
We can now find T on (3) using all the values we have:

`T= (2.42*10^(-3)(0.85* 440)^2)/(0.45)`

`T=75.22 N`