Question

In a study of the accuracy of fast food​ drive-through orders, Restaurant A had 242 accurate orders and 55 that were not accurate. a. Construct a 90​% confidence interval estimate of the percentage of orders that are not accurate. b. Compare the results from part​ (a) to this 90​% confidence interval for the percentage of orders that are not accurate at Restaurant​ B: 0.171less thanpless than0.245. What do you​ conclude?

Answer 1

(a) The 90% confidence interval estimate of the percentage of orders that are not accurate in Restaurant A is (0.148, 0.222).

(b) Restaurant B has more proportion of not accurate orders.

Step-by-step explanation:

The (1 - α)% confidence interval for population proportion is:

`CI=\hat p\pm z_(\alpha/2)\sqrt{(\hat p(1-\hat p))/(n)}`

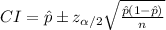
(a)

In Restaurant A the number of not accurate orders was x = 55 of n = 297 orders.

The sample proportion of not accurate orders in Restaurant A is:

`\hat p=(x)/(n)=(55)/(297)=0.1852`

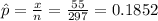
The critical value of z for 90% confidence level is:

`z_(\alpha/2)=z_(0.10/2)=z_(0.05)=1.645`

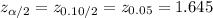
Compute the 90% confidence interval estimate of the percentage of orders that are not accurate in Restaurant A as follows:

`CI=\hat p\pm z_(\alpha/2)\sqrt{(\hat p(1-\hat p))/(n)}\\=0.1852\pm 1.645\sqrt{(0.1852(1-0.1852))/(297)}\\=0.1852\pm 0.0371\\=(0.1481, 0.2223)\\\approx (0.148, 0.222)`

Thus, the 90% confidence interval estimate of the percentage of orders that are not accurate in Restaurant A is (0.148, 0.222).

(b)

The 90% confidence interval estimate of the percentage of orders that are not accurate in Restaurant B is (0.171, 0.245).

The confidence interval for Restaurant B indicates that between 17.1% to 24.5% orders are inaccurate.

The values of this interval is more than that for Restaurant A.

So, it can be concluded that Restaurant B has more proportion of not accurate orders.