Question

You hang an object with mass m = 0.380 kg from a vertical spring that has negligible mass and force constant k = 60.0 N/m. You pull the mass down to a distance 0.030 m from its equilibrium position and release it. You measure the period of the subsequent motion to be 0.500 s.(a) If you pull the mass down0.010 mfrom its equilibrium position and release it, the new period would be which of the following?less than 0.500 s0.500 s greater than 0.500 sThere is no way to tell.(b) If, instead, you change the spring to one with a force constant of56.0 N/m but keep everything else the same, the new period will be which of the following?less than 0.500 s0.500 s greater than 0.500 sThere is no way to tell.(c) If, instead, you change the hanging object to one with a mass of0.530 kg but keep everything else the same, the new period will be which of the following?less than 0.500 s0.500 s greater than 0.500 sThere is no way to tell.

Answer 1

a) 0.500 s

b) greater than 0.500 s

c) greater than 0.500 s

Step-by-step explanation:

The time period of an oscillating spring-mass system is given by:

`T=2\pi \sqrt{(m)/(k)}`

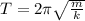
where, m is the mass and k is the spring constant.

a) As the period of oscillation does not depend on the distance by which the mass is pulled, the period would remain same as 0.500 s for the given system.

b) As the period varies inversely with the square root of spring constant, so with the decrease in the spring constant, the period would increase. So, the new period would be greater than 0.500 s.

c) As the period varies directly with the square root of mass, so with the increase in mass, the period will also increase. The new period will be greater than 0.500 s.