Answer:
a) Let X the random variable that represent the scores of a population, and for this case we know the distribution for X is given by:
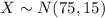
Where
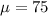 and
and
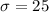
The distribution for the sample mean
 is given by:
is given by:

b)
 represent the true average for the scores of the aptitude test
represent the true average for the scores of the aptitude test
c) We can calculate the z scores and we got:
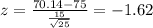

And we can calculate the probability with this difference:
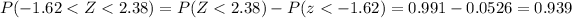
d) We can calculate the z scores and we got:
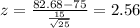
And we can calculate the probability with this difference:

e) We can calculate the z scores and we got:
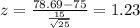
And we can calculate the probability with this difference:

Explanation:
a. What are the expected value, the standard deviation, and the shape of the sampling distribution of
 ?
?
Previous concepts
Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".
The Z-score is "a numerical measurement used in statistics of a value's relationship to the mean (average) of a group of values, measured in terms of standard deviations from the mean".
Let X the random variable that represent the scores of a population, and for this case we know the distribution for X is given by:
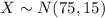
Where
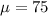 and
and
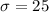
The distribution for the sample mean
 is given by:
is given by:

b. What is the random variable in this problem? Define it in words.
 represent the true average for the scores of the aptitude test
represent the true average for the scores of the aptitude test
c. What is the probability that the average aptitude test score in the sample will be between 70.14 and 82.14?
We can calculate the z scores and we got:
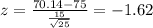

And we can calculate the probability with this difference:
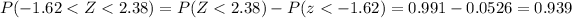
d. What is the probability that the average aptitude test score in the sample will be greater than 82.68?
We can calculate the z scores and we got:
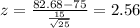
And we can calculate the probability with this difference:

e. What is the probability that the average aptitude test score in the sample will be less than 78.69?
We can calculate the z scores and we got:
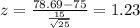
And we can calculate the probability with this difference:
