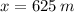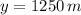Question

A rectangular plot of farmland will be bounded on one side by a river and on the other three sides by a​ single-strand electric fence. With 2500 m of wire at your​ disposal, what is the largest area you can​ enclose, and what are its​ dimensions?

Answer 1

`A = 781250\,m^(2)`,
`x = 625\,m`,
`y = 1250\,m`

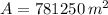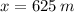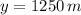
Explanation:

The perimeter covered by the electric fence in meters is:

`2\cdot x + y = 2500`

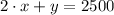
The area of the rectangle is:

`A = x\cdot y`

`A = x \cdot (2500-2\cdot x)`

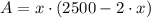
Let differentiate the previous equation and equates to zero:

`2500-4\cdot x = 0`

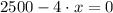
The critical point is:

`x = 625\,m`

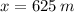
By the Second Derivative Text, it is proved that critical point lead to a maximum:

`(d^(2)A)/(dx^(2)) = -4`

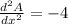
The other side of the rectangle is:

`y = 1250\,m`

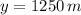
The largest area than can be enclosed is:

`A = (625\,m)\cdot (1250\,m)`

`A = 781250\,m^(2)`

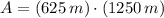
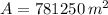
The dimensions of the triangle are:

`x = 625\,m`

`y = 1250\,m`