Question

The offices of​ president, vice​ president, secretary, and treasurer for an environmental club will be filled from a pool of 15candidates. Eightof the candidates are members of the debate team.​(a) What is the probability that all of the offices are filled by members of the debate​ team?​(b) What is the probability that none of the offices are filled by members of the debate​ team?

Answer 1

a) 5.13% probability that all of the offices are filled by members of the debate​ team

b) 2.56% probability that none of the offices are filled by members of the debate​ team

Explanation:

A probability is the number of desired outcomes divided by the number of total outcomes.

The order in which the people are chosen is important, since the first person is the president, the second is the vice president and so on... So we use the permutations formula to solve this question.

Permutations formula:

The number of possible permutations of x elements from a set of n elements is given by the following formula:

`P_((n,x)) = (n!)/((n-x)!)`

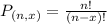
​(a) What is the probability that all of the offices are filled by members of the debate​ team?​

Desired outcomes:

4(president, vice​ president, secretary, and treasurer) offices from a set of 8(candidates of the members debate team).

So

`D = P_((8,4)) = (8!)/((8-4)!) = 1680`

Total outcomes:

4 offices from a set of 15 candidates.

`T = P_((15,4)) = (15!)/((15-4)!) = 32760`

Probability:

`P = (D)/(T) = (1680)/(32760) = 0.0513`

5.13% probability that all of the offices are filled by members of the debate​ team

(b) What is the probability that none of the offices are filled by members of the debate​ team?

Desired outcomes:

4(president, vice​ president, secretary, and treasurer) offices from a set of 7(candidates who are not of the members debate team).

`D = P_((7,4)) = (7!)/((7-4)!) = 840`

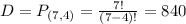
Total outcomes:

4 offices from a set of 15 candidates.

`T = P_((15,4)) = (15!)/((15-4)!) = 32760`

Probability:

`P = (D)/(T) = (840)/(32760) = 0.0256`

2.56% probability that none of the offices are filled by members of the debate​ team