a)
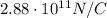
b)
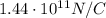
c)
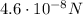
Step-by-step explanation:
a)
The magnitude of the electric field produced by a single-point charge is given by the equation
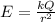
where
k is the Coulomb's constant
Q is the charge source of the field
r is the distance from the charge
The field has direction:
- Out from the charge if the charge is positive
- Towards the charge if the charge is negative
In this part, we want to find the electric field due to the alpha particle at the location of the electron. We have:
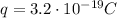 (charge of the alpha particle)
(charge of the alpha particle)
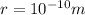 distance of the electron from the alpha particle
distance of the electron from the alpha particle
So, the electric field is
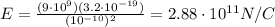
And since the alpha particle is positively charged, the direction of the field is out from the particle.
b)
Here we want to find the electric field due to the electron at the location of the alpha particle.
We use again the same formula as before:
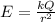
where
k is the Coulomb's constant
Q is the charge source of the field
r is the distance from the charge
where in this case:
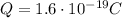 is the charge of the electron
is the charge of the electron
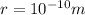 distance of the alpha particle from the electron
distance of the alpha particle from the electron
Therefore, the electric field due to the electron is
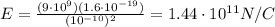
And since the electron is negatively charged, the direction of the field is towards the electron.
c)
The electrostatic force between two electric charges is given by Coulomb's Law:

where
k is the Coulomb's constant
q1, q2 are the two charges
r is the separation between the two charges
In this problem we have:
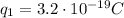 is the charge of the alpha particle
is the charge of the alpha particle
 is the charge of the electron
is the charge of the electron
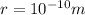 distance between the two charges
distance between the two charges
So, the force is
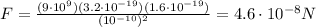
The force is the same on the two particles (Newton's third law of motion), and it is attractive, since the two charges have opposite sign.