Question

A scoop of ice cream has 1.5 inch radius. How talk should the cream cone of the same radius be in order to contain all of the ice cream inside the cone

Answer 1

The cream cone should be 6 inches.

Explanation:

Given:

A scoop of ice cream has 1.5 inch radius.

Now, to find the height of the cream cone.

So, we need to get the volume of scoop by putting formula:

Radius (r) = 1.5 inch.

Using the value π = 3.14.

`Volume=(4)/(3) \pi r^3`

`Volume=(4)/(3)* 3.14* 1.5^3\\\\Volume=(4)/(3)* 3.14* 3.375\\\\Volume=14.13\ inches^3.`

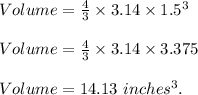
Thus, the volume of the ice cream scoop is 14.13 cubic inches.

So, to put all of the ice cream inside the cone.

We take the cream cone volume as the scoop volume.

Let the height of cone be
`h.`

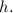
As, given radius is same.

Now, to get the height of the cream cone we put formula of volume:

`Volume=\pi r^2(h)/(3)`

`14.13=3.14 * (1.5)^2* (h)/(3)\\\\14.13=3.14* 2.25* (h)/(3)`

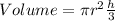
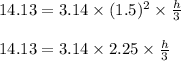
Multiplying both sides by 3 we get:

`42.39=3.14* 2.25* h\\\\42.39=7.065* h`

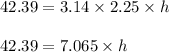
Dividing both sides by 7.065 we get:

`6=h`

`h=6\ inches.`

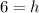
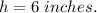
Hence, the height of the cone = 6 inches.

Therefore, the cream cone should be 6 inches.