Question

A 5.00-kg mass on the end of a light string rotates in a circular motion on a horizontal frictionless desk. The radius of the circle is 0.800 m. The string has a breaking strength of 50.0 N. What is the fastest rotational speed of the mass that will not break the string?

Answer 1

The fastest rotational speed of the mass is
`3.536s^(-1)`.

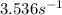Step-by-step explanation:

Here the string's breaking strength of 50.0 N means that the centripetal force exerted on the 5.00kg mass cannot exceed 50.0N—if it does, the string would break.

Therefore, we demand that

`(1).\;\: (mv^2)/(R) = 50.0N`

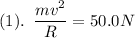
where
`m = 5.00kg`,
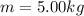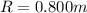`R = 0.800m` is the radius of the circle (also the length of the string), and
`v` is the tangential velocity of the mass.

Now, the tangential velocity can be written in terms of the rotational speed
`\omega` as follows:

`(2).\;\: v = \omega R`,

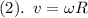and putting that into equation (1) we get:

`(m(\omega R )^2)/(R) = 50.0N`

`m \omega^2 R = 50.0N`,

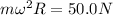and we solve for the rotational speed
`\omega` to get:

`\omega = \sqrt{(50N)/(mR) }.`

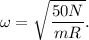
Finally, we out in the numeral values and get;

`\omega = \sqrt{(50N)/((5.00kg)(0.800m)) }.`

`\boxed{\omega = 3.536s^(-1)}`

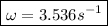
which is the fastest rotational speed of the mass.