Question

A 10.0 kg block is at rest on a frictionless horizontal table. A student applies a constant 40.0 N force at an angle of 60.0 degrees, as shown in the figure below. The block remains in contact with the table as it is dragged along.

a) How far does the block move in 5.00 seconds? b) How much work is done by the applied force? c) What is the speed of the block after 5.00 seconds? d) What is the kinetic energy of the block after moving this distance? e) Compare the answers for b and d. If the answers are the same, explain. If they differ,
explain why they differ.

Answer 1

See explanation.

Step-by-step explanation:

The horizontal component of the force is

`F_x = 40*cos(60^o) \\\\\boxed{F_x = 20N.}`

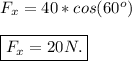
And the acceleration that this force causes in the 10.0 kg block is

`a = (F_x)/(m)`

`a = (20N)/(10.0kg)`

`\boxed{a = 2ms^(-2)}`

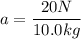
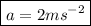
(a).

The distance
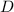`D` the block moves in time
`t` is

`D = (1)/(2)at^2;`

therefore, at
`t = 5.00s`

`D = (1)/(2)(2)(5)^2`,

`\boxed{D = 25.}`

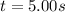
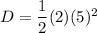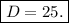
(b).

The work
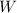`W` done by the applied force is

`W = F_xD`

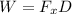
putting in numbers we get:

`W = 20N* 25m\\\\\boxed{W = 500J}`

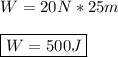
(c).

Those 500J of energy must appear as the kinetic energy of the block:

`(1)/(2)mv^2 = 500J`

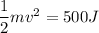
solving for
`v`, we get:

`v = \sqrt{(2*500J)/(m) }`

`v = \sqrt{(2*500J)/(10kg) }`

`\boxed{v =10ms^(-1)}`

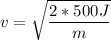
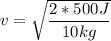
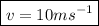
(d).

From (c), we know that the work done by he force must appear as the kinetic energy of the block; therefore, the kinetic energy of the block its 500J.

(e).

The kinetic energy of the block equals the work done by the force because of the law of conservation of energy, which here demands that the block cannot gain additional energy except that imparted by the force exerted on it.