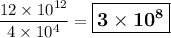2 Answers

Koras · Answer 1 · 2021-01-13T21:54:45+0000

Answer:

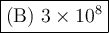
$\large \boxed{\text{(B) } 3* 10^(8)}$

Explanation:

To figure out how many times a number is than another, you divide the larger number by the smaller.

Here, your numbers are expressed in scientific notation, so you

1. Divide the coefficients and the exponentials separately

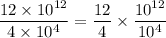
(12 * 10^(12))/(4 * 10^(4)) = (12)/(4) * (10^(12))/(10^(4))

2. Divide the coefficients

(12)/(4) = 3

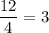
3. Divide the exponentials

Subtract the exponent in the denominator from the exponent in the numerator.

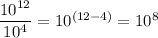
(10^(12))/(10^(4)) = 10^((12 - 4)) = 10 ^(8)

4. Re-join the new coefficient and the new exponential

$(12 * 10^(12))/(4 * 10^(4)) = \large \boxed{\mathbf{3* 10^(8)}}$

Please log in or register to add a comment.