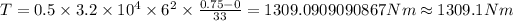Answer:
1309.1 Nm
Step-by-step explanation:
Torque is given as a product of Moment of innertia and acceleration hence
T=Ia where T is torque and a is acceleration
To get acceleration, it is rate of change of speed per unit time hence
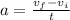 where v and t represent velocity and time respectively while subscripts f and i represent final and initial respectively. Also, I is given by
where v and t represent velocity and time respectively while subscripts f and i represent final and initial respectively. Also, I is given by
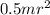 where m js mass and r is radius hence the net torque can now be written as
where m js mass and r is radius hence the net torque can now be written as
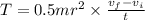
By substituting the given figures then