Question

Using the quadratic formula to solve x2 + 20 = 2x, what are the values of x?

1+ V21
O-17 191
O 1+2./197
O 17 191

Answer 1

by Quadratic formula ,
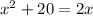`x^2 + 20 = 2x` , values of x are
`x = 1 \pm (1)i√(19)}` . None of mentioned options are correct according to question!

Explanation:

Here we have , expression x2 + 20 = 2x or ,
`x^2 + 20 = 2x` .

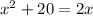We know that Quadratic formula is :

`x = \frac{-b \pm \sqrt{b^(2)-4ac}}{2a}`

`x^2 + 20 = 2x`

⇒
`x^2-2x+20=0`

`a=1\\b=-2\\c=20`

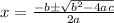
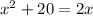
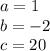
Putting this value in equation
`x = \frac{-b \pm \sqrt{b^(2)-4ac}}{2a}` :

⇒
`x = \frac{-b \pm \sqrt{b^(2)-4ac}}{2a}`

⇒
`x = \frac{-(-2) \pm \sqrt{(-2)^(2)-4(1)(20)}}{2(1)}`

⇒
`x = (2 \pm √(4-80))/(2)`

⇒
`x = ((2 \pm 2i√(19))/(2))`

⇒
`x = 1 \pm (1)i√(19)}`

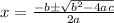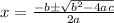
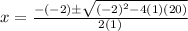
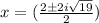
Therefore , by Quadratic formula ,
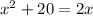`x^2 + 20 = 2x` , values of x are
`x = 1 \pm (1)i√(19)}` . None of mentioned options are correct according to question!