Question

Determine whether the three points are collinear. (3, -10), (-2, -7), (0, -5)

Answer 1

The points are not collinear.

Solution:

Let A, B and C be (3, -10), (-2, -7) and (0, -5).

If slopes of any two points are same, then the points are collinear.

Slope formula:

`$m=(y_2-y1)/(x_2-x_1)`

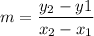
Slope of AB:

`$m_1=(-7-(-10))/(-2-3)`

`$m_1=(-7+10)/(-5)`

`$m_1=-(3)/(5)`

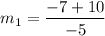
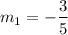
Slope of BC:

`$m_2=(-5-(-7))/(0-(-2))`

`$m_2=(-5+7)/(2)`

`$m_2=(2)/(2)`

`m_2=1`

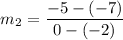
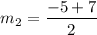
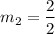
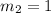
Slope of CA:

`$m_3=(-10-(-5))/(3-0)`

`$m_3=(-10+5)/(3)`

`$m_3=-(5)/(3)`

`m_1\\eq m_2 \\eq m_3`

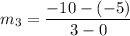
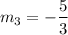
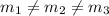
Slope of AB ≠ Slope of BC ≠ Slope of AC

Therefore the points are not collinear.